公用设施的费用该怎么样分摊？谁都想减少自己的开支，没有哪个选项能获得全体一致赞同。

  用多数决让某个人支付全款也有失妥当。即便是公用设施，每个人从中获取的利益也各不相同。这类问题是需要一种容易接受且公平的费用分摊方法。

  我们能够最终靠一则公寓电梯维修的事例思考这样的一个问题。对应提出的是沙普利值（Shapley value），一种按所得利益分配的支付方法。

  某日的《东京新闻报》上刊登了一篇题为“多数决的悖论”的评论。这篇法学家野村修也的投稿讲述了一个有关公寓公共设施费用分担的轶事。现将主要内容总结如下。

  一栋5 层高的公寓要对电梯做维修。公寓自治会上正在热议这样的一个问题。平时不用电梯的1 层住户拒绝承担维修费，讨论迟迟得不出结果。这时，5 层的住户想出一个歪点子，提议“让1 层住户负担全额费用”。这一提议在多数决中得到了2 层到5 层住户的一致赞成，最终以80% 的得票率获得通过。

  一栋5 层高的公寓要对电梯做维修。公寓自治会上正在热议这样的一个问题。平时不用电梯的1 层住户拒绝承担维修费，讨论迟迟得不出结果。这时，5 层的住户想出一个歪点子，提议“让1 层住户负担全额费用”。这一提议在多数决中得到了2 层到5 层住户的一致赞成，最终以80% 的得票率获得通过。

  这大概不是真实事件，只是有关多数决滥用的一个故事。那么，在这则故事中，多数决是如何被滥用的呢？

  多数决的对象必须有关全体的共同利益。然而在谁来支付费用的问题上，人们的利益是相悖的。再者，每层住户从电梯中获得的利益也大不相同。1 层住户乘坐电梯的机会很少，把维修费用全部推给他们是极不合理的决定。

  亚里士多德曾提出公正的标准：“平等的人应受平等的对待，不平等的人应受不平等的对待”，

  电梯等公寓公共设施的维修费用通常来源于各户每月缴纳的管理费所形成的资金池。而如今的普遍观念是，管理费金额取决于专有面积，和层数无关。因此，不管是1 层住户还是最高层的住户，如果专有面积相等，就要同等负担电梯的维修费用。

  曾经有一栋公寓的1层住户告到东京地方法院，认为“电梯的维修费用应该由2 层以上的住户支付”。但是这一申诉被驳回了。法院给出的理由是：1 层住户也能够正常的使用电梯，而且电梯是公寓作为整体所必不可少的一部分。

  我们先来关注“1层住户也能够正常的使用电梯”，即电梯的使用权。从电梯使用权人人平等的角度来说，的确所有住户都是平等的。不过，不同楼层的住户使用电梯的区间大不相同。住在10 层公寓4层的住户通常只使用电梯的“1～4层”。

  有了驾照和汽车，谁都可以上高速公路。即便如此，高速公路还是采取了受益者负担的原则，向使用高速公路的人使用费。如果电梯费用分摊的问题也采用受益者负担的原则，每层住户所得的利益不同，负担的金额理应不同。因此，在“使用权平等，负担平等”的同时，还要考虑到“受益不平等，负担也不平等”的一面。那么，不平等的这部分负担该怎么样计算呢？

  我们可以用“博弈论”的见解思考费用分摊的问题。博弈论是一门研究人类集体行为的学问，由冯·诺依曼（John vonNeumann）和摩根斯特恩（Oskar Morgenstern）于1944 年出版的大作《博弈论和经济行为》（Theory of Games and Economic Behavior）奠定了基础。费用分摊是它的一种应用。

  1974 年，博弈理论家利特柴尔德(Littlechild) 和欧文(Owen)探讨了分摊机场跑道建设成本的“机场博弈”问题。在不同层之间移动的电梯和飞机起降所用的跑道虽然有很大差异，但从费用分摊的角度来看又有很多相似之处，即谁也不会使用它的全部。

  机场博弈探讨了建设一条跑道的情况。使用跑道的是航空公司A、B 和C。每家公司起降的飞机型号不相同，公司A是小型机，公司B是中型机，公司C是大型机。机型越大，需要的跑道越长。因此，公司A只需要短跑道就能使飞机顺利起降，而公司B需要中等长度的跑道，公司C则需要长跑道。

  要满足三家公司的需求，必须建造一条公司C所需要的长跑道。可是，公司A和公司B都不需要那么长的跑道。

  假设建设短跑道所需的成本是12亿日元，中跑道需要18亿日元，长跑道需要23亿日元。也就是说，满足公司C的大型机的需求要花费23亿日元。

  计算与贡献相应的利益或与受益相应的负担的分配时，能够正常的使用沙普利值(Shapley value)。这种计算方式很好地体现了“平等的人应受平等的对待，不平等的人应受不平等的对待”。沙普利值的计算通常很复杂，但机场博弈是个例外，算法简单易懂。

  ［部分B］ 公司B 和C 使用的部分，即短跑道延长至中跑道所增加的部分。

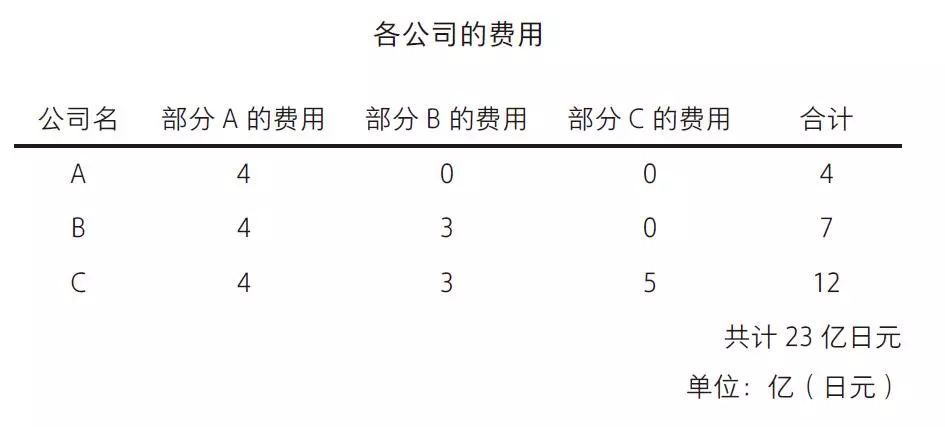
  首先，部分A 是A、B、C 三家公司都使用的部分，因此把12 亿日元的建设成本均分成三份，每家公司分别出4 亿日元。这种做法对平等的事物给予了平等对待。

  部分B 是B 和C 两家公司使用的部分，因此把部分A 延长出来的部分所需的6 亿日元（=18 亿日元-12 亿日元）成本均分成两份，公司B 和C 各出3亿日元。公司A 则一分不出。公司B和C 虽然得到了平等对待，但它们和公司A的待遇不同。因为公司A不使用部分B，和公司B、C 之间有不平等。

  部分C只有公司C 使用。因此，部分B延长出来的部分所需的5亿日元成本（=23 亿日元-18 亿日元）由公司C全额支付。公司C和不使用该部分的公司A和B的待遇不同。而公司A和B的支付额相同，均为0日元。

  C1 到C4 的各项费用由电梯修东西的人得出。不过，只维修电梯的一部分是不切实际的。比如，不可能“只维修2～3 层的部分”。那么，该如何得出2～3 层的维修费用呢？一个方案是通过设想推算出相当于C2 的金额。

  例如，设想“公寓只有2 层时电梯的维修费用”，得出的值便是C1。然后，设想“公寓只有3 层时电梯的维修费用”，得出的值是C1+C2。也就是说，将设想公寓只有3 层和2 层时的差额设为C2。

  同理，“公寓只有4 层时电梯的维修费用”为C1+C2+C3。设想公寓只有4 层，它和3 层的差额为C3。

  这样一来，支付总额正好是C=C1+C2+C3+［C-（C1+C2+C3）］，刚好凑齐实际所需的维修费用C。至于各层的负担金额该如何分摊到该层住户的头上，如果按照现行制度，就要由各户根据专有面积支付相应比例。

  但是，光用沙普利值决定费用分摊是否有失公允？就算1层住户从来不用电梯，是否也从正常运作的电梯中获得了利益呢？

  上文介绍的东京地方法院给出的理由是“电梯是公寓作为整体所必不可少的一部分”。如果公寓的电梯一直故障没人修理，即便1层住户不使用电梯，资产价值也会下滑。搞不好还会使公寓演变成贫民楼。

  （2） 电梯可提升公寓整体的安全保障价值。正如东京地方法院所言，这可以视为各层住户的共同利益。

  在费用分摊中，（1）对应沙普利值，（2）对应均摊。将二者合二为一的方法便是把电梯维修费用的总额分成两部分，一部分按沙普利值走，另一部分按均摊走。这种方法在数学上叫作“凸组合”。

  为了让说明更简单，我们以每层只有1 户住户的3 层公寓为例来讲解凸组合的应用。设维修费用总额C=48。首先计算沙普利值。

  设1～2 层的维修费用C1 为36。这些费用由2 层住户负担18，3 层住户负担18。

  设2～3 层的维修费用C2 为12（48-36）。这部分费用全部由3 层住户负担。

  于是，各层的负担金额分别为1 层负担为零，2 层负担18，3层负担18+12=30。这便是沙普利值得出的结果。

  现在，假设我们考虑到（2）的价值，将总费用的50%，即24 用均摊原则进行分配。用层数3 除总费用的一半24，得出每层各负担8。将沙普利值减至一半后，1 层仍为0，2 层为9，3 层为15。在每层的均摊的基础上加上减至一半的沙普利值，得出：

  这是将比例控制在50% 时，沙普利值和均摊的凸组合的值。即使比例不是50%，这个值也可以用相同的算法得出。

  那么，用凸组合把沙普利值和均摊结合到一起时，该怎么样决定二者的比例？从维修费用全部均摊的0%，到全部按沙普利值走的100%，摆在我们面前的选项有很多。

  如果一个人出于某个原因提出一个方案并得到大家的赞同，那就敲定了。比如，某人认为“电梯本身的便捷性和它为公寓价值提升所做的贡献都很重要，我们就五五分吧”，据此提出50%。或者根据现行制度所说的“1层住户也平等享有电梯的使用权”，提议将沙普利值的比例降为0%。比例的数值很难只根据原理原则做出决定。原理原则比较宽泛，不具备决定这种细节的调节功能。于是，我们不思考哪种比例是正确的，而思考哪种比例或者哪种选择方法最容易让人们接受。

  假设现在每个人心中都有一个最佳比例点。当比例低于这个点时，会感到“沙普利值的比例过低”；当比例高于这个点时，会感到“沙普利值的比例过高”。我们称其为峰值。

  如果3 个人的峰值为“10%，30%，50%”，就选择正中间的30%；即便3 个人的峰值变成“10%，30%，100%”，正中间依然是30%。就算有人故意给出极端的数字，也无法按自己的意愿诱导结果。

  在“10% 对30%”的多数决中，峰值是50% 的人会转向支持30%，因此30% 将以2 比1 胜出。在“30% 对50%”的多数决中，峰值是10% 的人会转向支持30%，故30% 将以2 比1 胜出。

  对于排列成一行的选项来说，选择中位数选项——中间规则是最佳的决策方法。这样做不仅能避免投票者通过极端回答诱导结果，还能选出全胜者。全胜者的性质使它代表了实际多数意见，而且“正中间”的选项容易让大家理解这是共同妥协让步的结果，也更加容易让投票者接受。